Domino Data Lab

AUGUST 1, 2021

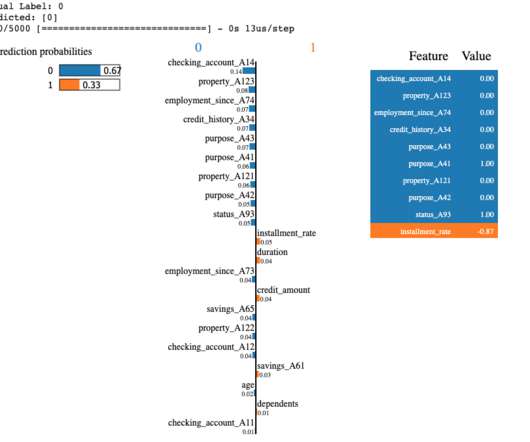
In this article we cover explainability for black-box models and show how to use different methods from the Skater framework to provide insights into the inner workings of a simple credit scoring neural network model. The interest in interpretation of machine learning has been rapidly accelerating in the last decade. See Ribeiro et al.

Modeling 139

Modeling Deep Learning Machine Learning Knowledge Discovery 139

The Unofficial Google Data Science Blog

JULY 22, 2020

One reason to do ramp-up is to mitigate the risk of never before seen arms. A ramp-up strategy may mitigate the risk of upsetting the site’s loyal users who perhaps have strong preferences for the current statistics that are shown. For example, imagine a fantasy football site is considering displaying advanced player statistics.

Experimentation 95

Experimentation Statistics Testing Strategy 95

Domino Data Lab

MAY 20, 2021

In this article we discuss why fitting models on imbalanced datasets is problematic, and how class imbalance is typically addressed. This renders measures like classification accuracy meaningless. This carries the risk of this modification performing worse than simpler approaches like majority under-sampling. Chawla et al.

Machine Learning 136

Machine Learning Metrics Data mining Knowledge Discovery 136

The Unofficial Google Data Science Blog

JANUARY 14, 2016

Of particular interest to LSOS data scientists are modeling and prediction techniques which keep improving with more data. Well, it turns out that depending on what it cares to measure, an LSOS might not have enough data. Being dimensionless, it is a simple measure of the variability of a (non-negative) random variable.

Experimentation 41

Experimentation Statistics Metrics Measurement 41

The Unofficial Google Data Science Blog

NOVEMBER 4, 2015

Posteriors are useful to understand the system, measure accuracy, and make better decisions. But most common machine learning methods don’t give posteriors, and many don’t have explicit probability models. In our model, $theta$ doesn’t depend directly on $x$ — all the information in $x$ is captured in $t$.

KDD 40

KDD Testing Machine Learning Modeling 40